Determinación de módulos elásticos de materiales compuestos mediante la Técnica de Excitación por Impulso
El propósito de esta sección es presentar la teoría y la metodología para la determinación no destructiva de los módulos elásticos de materiales compuestos. El siguiente contenido comprende una revisión de la literatura y los avances realizados por la ATCP Engenharia Física en la aplicación de la Técnica de Excitación por Impulso [1] para compuestos.
Introducción
La definición de materiales compuestos varía según el autor, dependiendo de los aspectos y consideraciones que se tomen en cuenta. Según Chawla [2], para ser clasificado como un material compuesto, un material debe cumplir con algunas condiciones. Primero, debe ser fabricado, es decir, debe ser proyectado y producido por el hombre; además, debe consistir en una adecuada combinación de distintas fases físicas y/o químicas; por último, sus características no son alcanzadas por ninguno de los componentes aislados.
Los materiales compuestos intrínsecos comprenden al menos dos componentes: la matriz, que puede ser cerámica, metálica o polimérica; y el refuerzo, que puede estar en forma de fibras o partículas. Los compuestos estructurales, por otro lado, pueden ser laminados o paneles sándwich (Fig. 1).
![Figura 1 - Clasificación de los materiales compuestos [3].](/images/F1-ES-Classification-composite-materials.jpg)
Figura 1 - Clasificación de los materiales compuestos [3].
El advenimiento de los composites de alta tecnología comenzó en la década de 1960 por la demanda de materiales con alta resistencia y baja densidad. Las principales áreas de aplicación incluyeron el sector de la construcción civil, la industria aeroespacial y la energía [2,4]. Actualmente, los materiales compuestos se utilizan en varias industrias y se emplean para fabricar una amplia gama de productos, desde artefactos simples hasta automóviles [5] y recipientes de alta presión (Fig. 2).

Figure 2 - Recipientes de alta presión para gas natural fabricados por 3M con materiales compuestos.
La caracterización de las propiedades elásticas de los composites es crucial para la correcta selección de materiales, simulaciones numéricas y cálculos estructurales fiables. Una de las técnicas no destructivas utilizadas para evaluar los módulos elásticos y que ha ido creciendo dentro de este sector es la Técnica de Excitación por Impulso, que es el tema central de esta sección. La figura 3 muestra especímenes de CFRP y UHMWPE preparados para la determinación del módulo de elasticidad mediante la Técnica de Excitación por Impulso.
![Figure 3 - Amuestras de una armadura balística de polietileno de ultra alto peso molecular (UHMWPE) y de un panel monolítico de plástico reforzado con fibra de carbono (CFRP) preparadas para la caracterización no destructiva de los módulos elásticos mediante la Técnica de Excitación por Impulso y los Sistemas Sonelastic® [6].](/images/F3-ES-Amuestras-UHMWPE-armadura-balistica-CFPR-fibra-carbono.png)
Figure 3 - Amuestras de una armadura balística de polietileno de ultra alto peso molecular (UHMWPE) y de un panel monolítico de plástico reforzado con fibra de carbono (CFRP) preparadas para la caracterización no destructiva de los módulos elásticos mediante la Técnica de Excitación por Impulso y los Sistemas Sonelastic® [6].
Determinación de los módulos elásticos de compuestos aplicando la IET
Fundamentos de la técnica
La Técnica de Excitación por Impulso [1] consiste en determinar los módulos elásticos de un material a partir de las frecuencias naturales de vibración de una o más probetas de geometría regular (barra, cilindro, disco o anillo). Estas frecuencias son excitadas por un impulso mecánico de corta duración, seguido de la adquisición de una respuesta acústica con un sensor acústico. Posteriormente se realiza un procesamiento matemático para obtener el espectro de frecuencias. Los módulos elásticos dinámicos se calculan utilizando ecuaciones proporcionadas por la norma ASTM [1], que considera la geometría, la masa, las dimensiones y las frecuencias identificadas en el espectro de respuesta acústica [1].
Para la excitación del modo de vibración requerida, es necesario imponer condiciones de contorno específicas. La figura 4 muestra un soporte de muestra con dispositivo de impulso automático y sensor acústico posicionado para medir el módulo de Young de una barra rectangular en modo de vibración de flexión.
![a) Montaje básico para la caracterización de una barra en modo de vibración a flexión utilizando la Técnica de Excitación por Impulso [7]](/images/F4-A-ES-Montaje-caracterizacion-barra-flexion-tecnica-excitacion-impulso.png)

Figura 4 - a) Montaje básico para la caracterización de una barra en modo de vibración a flexión utilizando la Técnica de Excitación por Impulso [7] y b) SA-BC: Soporte regulable para barras y cilindros con probeta de composite aeronáutico.
Modos de vibración
Una muestra puede vibrar en diferentes modos y para cada modo hay una frecuencia fundamental específica. La figura 5 muestra los principales modos de vibración fundamentales [8].
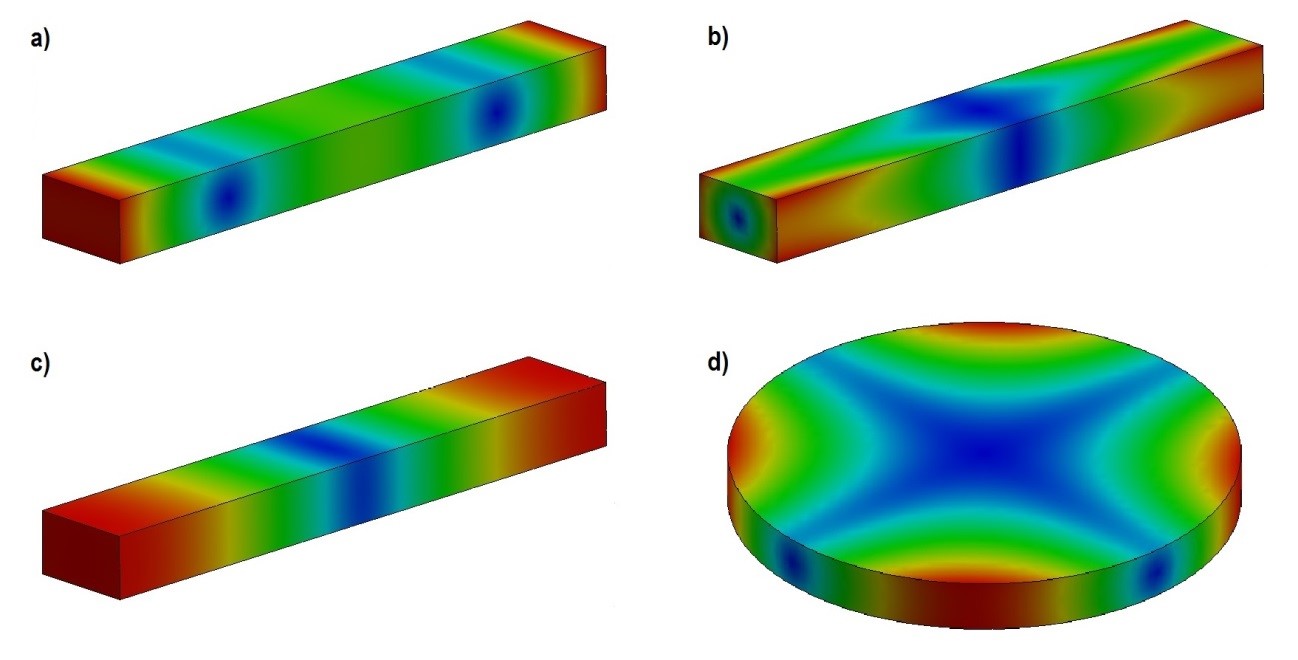
Figura 5 - Modos fundamentales de vibración: a) Flexional, b) Torsional, c) Longitudinal y d) Planar. Las áreas azules representan las regiones de mínima amplitud de vibración, mientras que las áreas rojas representan las regiones de máxima amplitud de vibración.
Las frecuencias naturales de estos modos dependen de la geometría, la masa, las dimensiones y los módulos elásticos. Las condiciones de contorno determinan el modo de vibración. Las Figuras 6a-c [1] muestran las condiciones de contorno óptimas para los principales modos de vibración de una barra rectangular, mientras que la Figura 6d muestra lo mismo para un disco. Con base en las frecuencias de resonancia de la muestra y empleando las ecuaciones de la norma ASTM E1876 [1], se calculan los módulos elásticos dinámicos correspondientes.
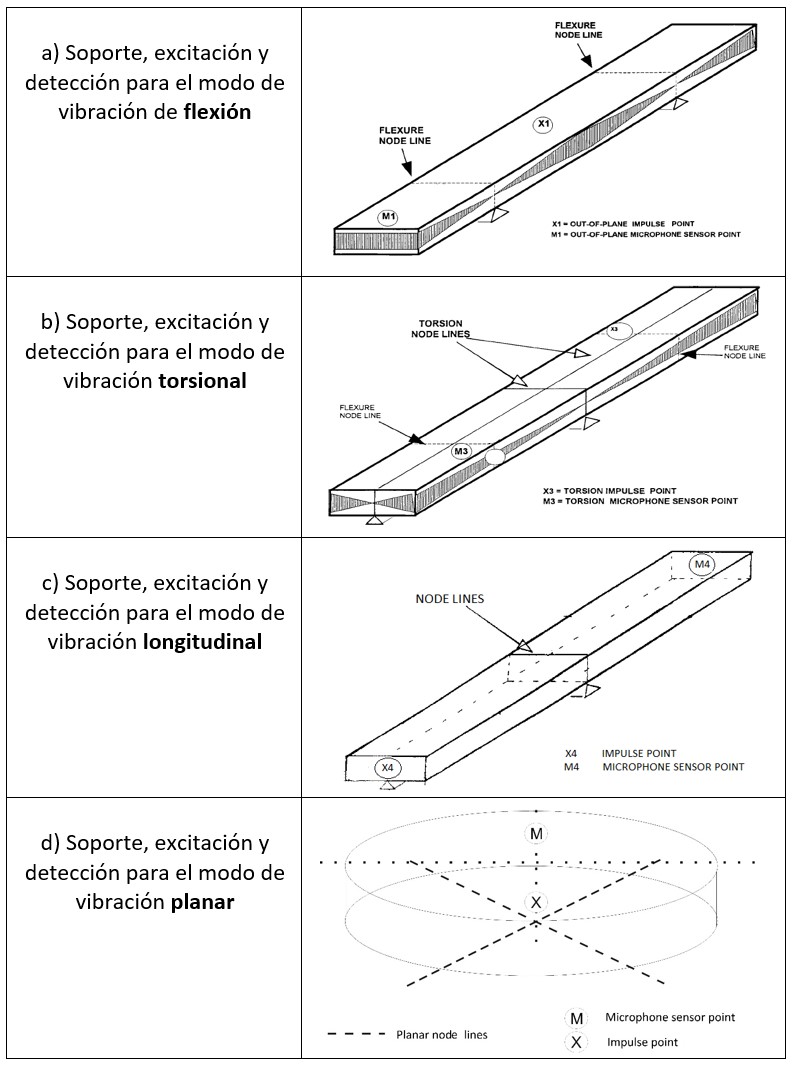
Figura 6 - Soporte, excitación y detección para los modos de vibración de (a) flexión, (b) torsión, (c) longitudinal y (d) planar.
Módulos elásticos de composites
La mayoría de los materiales compuestos muestran algún grado de anisotropía, es decir, sus propiedades dependen de la dirección de la tensión. En consecuencia, cuando se mide utilizando la técnica de excitación por impulso, es importante conocer e informar la simetría del material y la orientación de la muestra.
En el Apéndice A de nuestro Informativo Técnico-Científico ITC-06 se describe la teoría de la elasticidad aplicada a los materiales compuestos en base a planteamientos micro y macromecánicos generales para las tres simetrías principales. La Fig. 7 muestra una estructura genérica no isotrópica, de manera que, para la caracterización del módulo de elasticidad principal (E1, E2, E3) son necesarias tres probetas en las direcciones 1, 2 y 3).
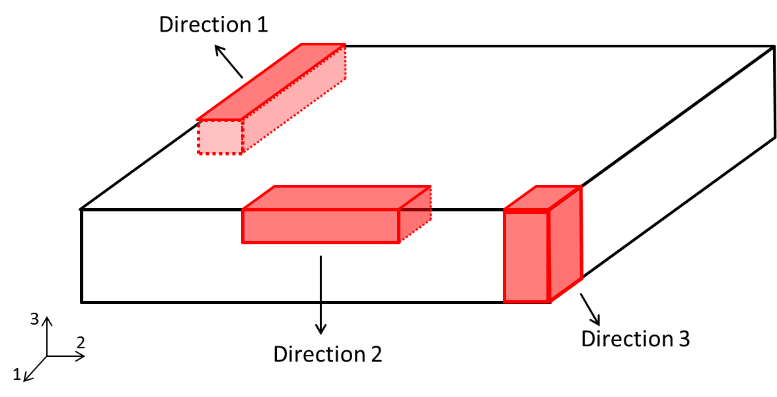
Figura 7 - Diagrama de una estructura genérica, detallando cómo obtener especímenes en las tres direcciones principales.
La Tabla 1 indica los módulos elásticos que se pueden determinar usando la Técnica de Excitación por Impulso y las pautas para una muestra ortotrópica (Figura 7). En esta tabla, los términos utilizados [9] se definen como:
E1 – Módulo de Young en la dirección 1;
E2 – Módulo de Young en la dirección 2;
E3 – Módulo de Young en la dirección 3;
Geff – Módulo de corte caracterizado por el equipo Sonelastic®. Este módulo consiste en combinar los módulos Gij mostrados entre paréntesis [14];
G13 – Módulo de corte asociado a las deformaciones en el plano 13;
G23 – Módulo de corte asociado a las deformaciones en el plano 23;
G12 – Módulo de corte asociado con las deformaciones en el plano 12.
Tabla 1 - Módulos elásticos medibles por la Técnica de Excitación por Impulso de acuerdo con la orientación de la muestra y los modos de vibración.

• El módulo de Young
-Por modo de vibración longitudinal
Cuando la muestra se carga en modo longitudinal (consulte las condiciones de contorno en la Figura 6c), el módulo de elasticidad medido estará en la dirección de la longitud de la muestra. Es decir, la orientación de la muestra determinará qué módulo se está midiendo (E1, E2, E3 o una composición de estas direcciones), como se muestra en la Tabla 1.
-Por modo de vibración de flexión
Cuando se flexiona un material, existen esfuerzos simultáneos de tensión y compresión, como se ilustra en la Figura 8 [10]. Para materiales homogéneos e isotrópicos, el módulo de elasticidad obtenido en un ensayo de flexión coincide con el módulo de elasticidad medido en dirección longitudinal. Por lo tanto, el módulo elástico dinámico obtenido a través del modo de vibración de flexión es el mismo que el obtenido a través del modo de vibración longitudinal [10]. Sin embargo, se sabe que, en flexión, la superficie del material es la región donde se presentan los valores más altos de tensión normal. Por esta razón, si la rigidez de la muestra es diferente en la superficie en comparación con el centro (por ejemplo, si hay un gradiente de rigidez a lo largo del espesor) o si la muestra tiene pequeños defectos superficiales como poros, grietas y microfisuras, habrá una discrepancia en los valores obtenidos por el modo flexional y longitudinal. Existen varios trabajos enfocados a la evaluación de maderas que reportan diferencias en los valores según el modo de vibración [8,11-13].
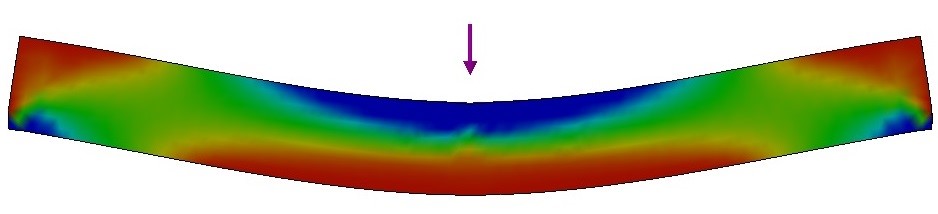
Figura 8 – Regiones de tensión (rojo) y compresión (azul) durante una prueba de flexión.
• Módulo de corte
-Modo de vibración torsional
Cuando un material se somete a un ensayo de torsión, dos valores del módulo de corte actúan concomitantemente sobre materiales transversalmente isótropos y ortótropos. Si existe una torsión como la descrita en la Figura 5b, el módulo de cortante obtenido estará asociado a las superficies que están siendo cortadas (las cuatro superficies laterales de la probeta). Por lo tanto, el módulo de corte calculado utilizando la frecuencia de vibración torsional fundamental corresponde a un módulo efectivo. Así, los resultados obtenidos por Sonelastic serán una combinación de los módulos de corte activos (la Tabla 1 indica los módulos de corte activos que componen el valor efectivo para cada orientación) [14].
• El coeficiente de Poisson>
La determinación del coeficiente de Poisson aplicando la Técnica de Excitación por Impulso es indirecta. Se realiza mediante la correlación entre el módulo de Young y el módulo de corte, o mediante la ecuación de la relación de Poisson recíproca. Las ecuaciones son de la Teoría de la Elasticidad y están directamente relacionadas con las matrices de rigidez y la simetría del material que se muestran a continuación:
-Material isotrópico:
-Material transversalmente isotrópico:
-Material ortotrópico:
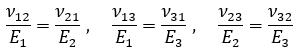
Donde: E es el módulo de Young, G el módulo de corte y ν la relación de Poisson de un material isotrópico. En el Apéndice B de nuestro Informativo Técnico-científico ITC-06 se describen la deducción de estas ecuaciones, así como explicaciones más detalladas sobre la medida del coeficiente de Poisson mediante la Técnica de Impulso de Excitación.
Simetría del material y módulos de elasticidad obtenidos por Sonelastic®
Como se mencionó anteriormente, los materiales compuestos pueden presentar diferentes tipos de simetría en cuanto a sus propiedades mecánicas. Por tanto, es necesario conocer la simetría, los módulos elásticos buscados y las orientaciones. La Tabla 2 muestra un resumen de la información presentada hasta este punto, incluyendo detalles de los módulos elásticos medibles por Sonelastic®.
Tabla 2 – Módulos elásticos según simetría, especímenes requeridos y módulos elásticos posibles de determinar con la Técnica de Excitación por Impulso (IET).
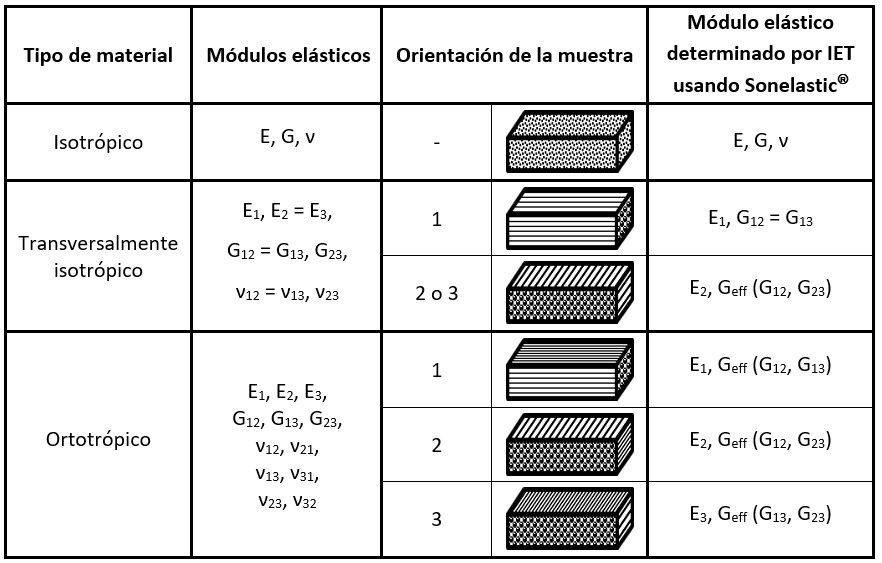
Para determinar los módulos elásticos de los materiales compuestos utilizando la Técnica de Excitación por Impulso es necesario preparar muestras con orientaciones específicas de acuerdo con la simetría del material. Cabe mencionar que también es posible medir muestras que contienen fibras en ángulos intermedios (entre 0º y 90º), de manera que las propiedades medidas en estas direcciones estén de acuerdo con la orientación de la muestra.
Consideraciones finales
Los módulos elásticos de los composites, materiales formados por la combinación de dos o más materiales de distinta naturaleza, pueden medirse de forma no destructiva mediante la Técnica de Excitación por Impulso utilizando los Sistemas Sonelastic. Para eso, es necesario conocer la simetría del compuesto para preparar especímenes de acuerdo con las direcciones del material.
Ejemplos de clientes y aplicaciones relacionadas con los composites.
Referencias
[1] ASTM International. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration. ASTM E1876-21. 2021.
[2] CHAWLA, K. K., Composite Materials: Science and Engineering. 3 ed. New York, Springer, 2012.
[3] Translated from: composite classification. Available at:
[4] DANIEL, I. M., ISHAI, O. Engineering Mechanics of Composite Materials. New York, Oxford University Press, 1994, 395 p.
[5] Pressure vessel for natural gas manufactured by 3M. Available at:
[6] Available at:
[7] Positioning and characterization scheme in accordance to ASTM E1876. Available at:
[8] HEYLIGER, P., UGANDER, P., LEDBETTER, H. Anisotropic Elastic Constants: Measurement by Impact Resonance. Journal of Materials in Civil Engineering, pp. 356-363, set/out 2001.
[9] Adapted from WANGAARD, F.F. The Mechanical Properties of Wood. New York: John Wiley & Sons, Inc, 1950.
[10] KAW, A.K. Mechanics of composite materials. 2 ed. Boca Raton, Taylor & Francis Group, 2006, 457 p.
[11] ROCHA, J.S., PAULA, E.V.C.M. de, SIQUEIRA, M.L. Flexão Estática em amostras pequenas livres de defeitos. Acta Amazonica, Manaus, p. 147-162. 1988.
[12] CHO, C.L., Comparison of Three Methods for Determining Young’s Modulus of Wood. Taiwan Journal for Science, pp. 297-306, Maio/2007.
[13] BUCUR, V., Acoustics of Wood. 2ª ed. Germany, Springer, 2006. p. 393.
[14] BODIG, J., JAYNE, B. A. Mechanics of wood and wood composites. Malabar (EUA), Krieger Publishing Company, 1993.
[15] GIBSON, R. F. Principles of composite material mechanics. USA, 1994, 425 p.
[16] CALLISTER Jr., W.D. Materials Science and Engineering. 7ª ed. New York: John Wiley & Sons, Inc, 2007.
[17] Translated from stress-strain graph. Available at:
< http://www.ctb.com.pt/?page_id=1471>. Accessed on July 8, 2014.
[18] NYE, J.F. Physical Properties of Crystals: their representation by tensors and matrices. Oxford: At the Clarendon Press. 1957.
[19] TSAI, S. W. Theory of Composites Design. Stanford: Stanford University, 2008, 230 p.
Descubra los Sistemas Sonelastic® :
Sistemas Sonelastic® para muestras pequeñasSistemas Sonelastic® para muestras medianas
Sistemas Sonelastic® para muestras grandes
Cotación para Sistema Sonelastic® personalizado


