Determinação dos módulos elásticos de madeiras e derivados empregando a Técnica de Excitação por Impulso
O objetivo desta seção é apresentar a teoria e a metodologia para a determinação não-destrutiva dos módulos elásticos de madeiras e derivados pela Técnica de Excitação por Impulso. O conteúdo a seguir compreende uma revisão da literatura e os avanços realizados na aplicação desta técnica, já normatizada para materiais isotrópicos [1], para a caracterização de madeiras.
Introdução
A madeira, tanto pela sua disponibilidade quanto pelas suas características, foi um dos primeiros materiais utilizados pelo homem para fins estruturais. Pode ser classificada como um composto sólido, orgânico, formado majoritariamente por celulose, cuja principal função é manter a sustentação das árvores [2]. É um material proveniente de caules que crescem anualmente em diâmetro e comprimento.
Além das aplicações estruturais, a madeira também é útil como matéria-prima para derivados como laminado colado, compensado laminado, placas de partículas e madeira composta com plásticos (WPC - Wood Plastic Composites).
![Figura 1 - Ponte localizada na floresta de Montmorency sobre o rio Montmorency, Quebec, Canadá. Possui vão de 44 m, altura de 33 m e largura de 4,8 m [3].](/images/F1-PT-Ponte-Estrutura-Madeira-Montmorency-Vao-Altura-Largura.jpg)
Figura 1 - Ponte localizada na floresta de Montmorency sobre o rio Montmorency, Quebec, Canadá. Possui vão de 44 m, altura de 33 m e largura de 4,8 m [3].
Devido às características microestruturais advindas de sua origem natural, as propriedades físicas da madeira dependem da direção de solicitação [2]. As três principais direções das madeiras estão ilustradas na Fig. 2 e listadas a seguir:
- Longitudinal (L): Direção paralela às fibras;
- Radial (R): Direção perpendicular aos anéis de crescimento;
- Tangencial (T): Direção tangencial aos anéis de crescimento.
![Figura 2 - Principais direções adotadas para madeiras [4].](/images/F2-PT-Direcoes-Madeira-Longitudinal-Radial-Tangencial.png)
Figura 2 - Principais direções adotadas para madeiras [4].
A madeira é classificada como um material ortotrópico por apresentar planos ortogonais de simetria nos quais as propriedades elásticas são constantes [5]. Esta classificação é uma aproximação, porque dependendo da propriedade avaliada, pode haver variações e gradientes ao longo de uma mesma direção, por exemplo, ao longo da direção radial e dos anéis de crescimento.
A determinação dos módulos elásticos é crucial para o desenvolvimento, a seleção e o controle de qualidade de madeiras e derivados, assim como para simulações e cálculos estruturais. Estas aplicações são possíveis devido à sensibilidade dos módulos elásticos à presença de descontinuidades, defeitos, rachaduras, nós, alterações microestruturais e à composição química [6]. Uma das técnicas não-destrutivas que vem crescendo no setor para a determinação dos módulos é a Técnica de Excitação por Impulso, foco desta página.
Determinação dos módulos elásticos de madeiras empregando a TEI
Fundamentos da técnica
A Técnica de Excitação por Impulso determina os módulos elásticos do material a partir das frequências naturais de vibração de um corpo de prova de geometria regular (barra ou cilindro). Estas frequências são excitadas por meio de um impacto mecânico de curta duração, seguido da captação da resposta acústica por um sensor acústico. Um tratamento matemático é aplicado no sinal para a obtenção do espectro de frequências. A partir disso, são calculados os módulos elásticos dinâmicos considerando a geometria, a massa, as dimensões do corpo de prova e as frequências obtidas com o processamento da resposta acústica.
Para a excitação e a detecção dos modos de vibração desejados é necessário impor condições de contorno específicas. Na Fig. 3 é apresentado um exemplo de suporte de corpos de prova de médio porte, com pulsador manual e captador acústico posicionados para excitar e detectar o modo de vibração flexional.
![a) Disposição para a caracterização de uma barra de madeira no modo de vibração flexional pela Técnica de Excitação por Impulso [8]](/images/F3-A-PT-Caracterizacao-barra-madeira-modo-vibracao-flexional-Tecnica-Excitacao-Impulso-modulo.png)

Figura 3 – a) Disposição para a caracterização de uma barra de madeira no modo de vibração flexional pela Técnica de Excitação por Impulso [8]; b) Suporte ajustável para barras e cilindros SA-BC com Captador Acústico CA-DP e pulsador manual desenvolvidos e fabricados pela ATCP Engenharia Física.
O módulo de Young obtido pela Técnica de Excitação por Impulso é dito dinâmico e sempre maior ou igual ao obtido pelo ensaio quase-estático. No entanto, é possível estabelecer uma correlação entre eles [7].
Modos de vibração
Um corpo de prova pode vibrar em diferentes modos e para cada um desses há uma frequência fundamental. Na Fig. 4 são apresentados alguns dos principais modos fundamentais de vibração [9].
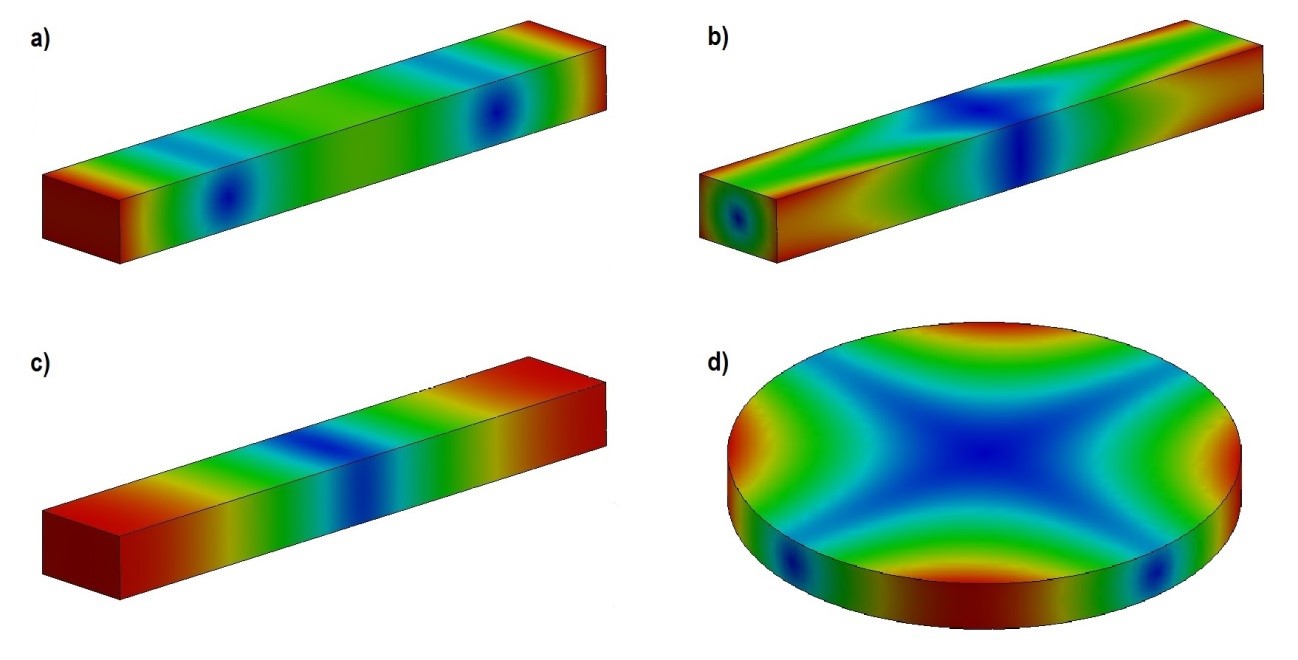
Figura 4 - Modos fundamentais de vibração: a) flexional, b) torcional, c) longitudinal e d) planar. As regiões em azul representam os pontos em que a amplitude de vibração é mínima, enquanto as regiões em vermelho representam as regiões em que a amplitude de vibração é máxima.
O que determina qual modo de vibração será excitado são as condições de contorno impostas ao corpo de prova. A frequência fundamental destes modos é uma função da geometria, da massa, das dimensões e dos módulos elásticos. Nas Figuras 5 a-c [1,6] são ilustradas as condições de contorno ótimas para os principais modos de vibração de uma barra [1], e na Figura 5 d, de um disco. A partir das frequências de ressonância do corpo de prova em determinados modos de vibração são calculados os módulos elásticos dinâmicos correspondentes.
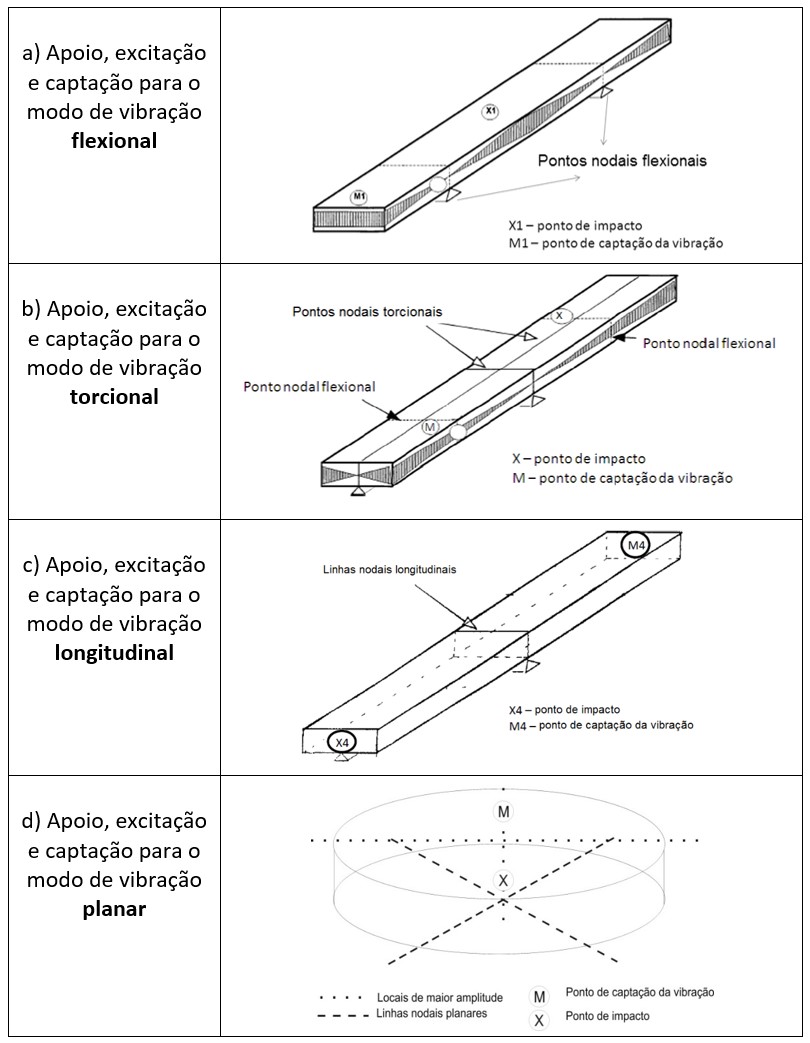
Figura 5 - Condições de contorno impostas ao corpo de prova de madeira ou derivado para a excitação do modo de vibração fundamental (a) flexional, (b) torcional, (c) longitudinal e (d) planar.
Os módulos elásticos das madeiras
As propriedades elásticas da madeira variam de acordo com a orientação das fibras e dos anéis de crescimento. Quando determinadas com a Técnica de Excitação por Impulso, é importante estar ciente da influência desta orientação para reportar os resultados corretamente. No caso dos derivados de madeira, a análise é análoga.
Tabela 1 – Módulos elásticos determináveis pela Técnica de Excitação por Impulso de acordo com a orientação da fibras e em função dos modos de vibração.

A Tabela 1 indica os módulos elásticos de madeiras que podem ser determinados empregando a Técnica de Excitação por Impulso em função da orientação do corpo de prova e do modo de vibração. Nesta tabela, os termos utilizados [5,10] são definidos por:
EL – Módulo de Young na direção longitudinal;
ET – Módulo de Young na direção tangencial;
ER – Módulo de Young na direção radial;
Gef – Módulo de cisalhamento efetivo determinado pelo Sistema Sonelastic®, corresponde a uma combinação dos módulos Gij entre parênteses [5];
GLT – Módulo de rigidez associado a deformações de cisalhamento no plano tangencial (LT) resultante do cisalhamento nos planos LR e RT;
GRT – Módulo de rigidez associado a deformações de cisalhamento no eixo transversal (RT) resultante do cisalhamento nos planos LR e LT;
GLR – Módulo de rigidez associado a deformações de cisalhamento no plano radial (LR) resultante do cisalhamento nos planos LT e RT.
• Módulo de Young
-Pelo modo de vibração longitudinal
Quando o corpo de prova for solicitado na direção longitudinal (ver condições de contorno na Fig. 5c), o módulo elástico determinado corresponde ao módulo de Young na direção do comprimento do corpo de prova (EL). A orientação da extração do corpo de prova é o que determinará o módulo obtido, como apresentado na Tabela 1 (EL, ER, ET ou uma composição destes no caso de amostras cuja direção paralela ao seu comprimento não coincida a uma das orientações principais).
- Modo de vibração flexional
Quando um material é flexionado, ocorrem solicitações simultâneas de tração e compressão, como ilustrado na Fig. 6 [11]. Para materiais homogêneos e isotrópicos, o módulo elástico determinado em um ensaio de flexão coincide com o módulo elástico determinado com um ensaio de tração na direção longitudinal. De forma similar, o módulo elástico dinâmico determinado pelo modo de vibração flexional é o mesmo que pelo modo de vibração longitudinal [11]. Entretanto, em flexão, a superfície do corpo de prova é submetida a tensões maiores que o centro. Por essa razão, caso a rigidez do corpo de prova seja diferente na superfície em comparação ao centro (por exemplo, se houver um gradiente de rigidez ao longo da espessura) ou caso a amostra apresente defeitos superficiais como poros, trincas e microtrincas, haverá uma discrepância nos valores determinados pelo modo de vibração flexional e longitudinal [10,12-14].
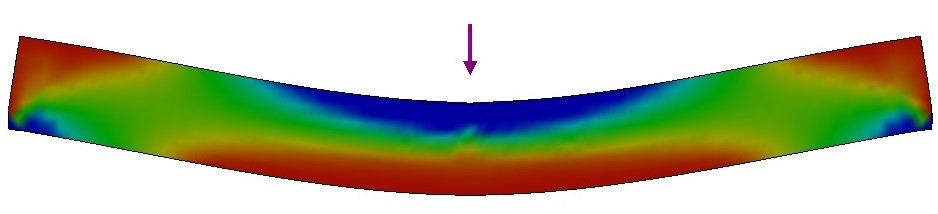
Figura 6 - Regiões sob tração (vermelho) e sob compressão (azul) durante um ensaio de flexão.
• Módulo de cisalhamento
-Pelo modo de vibração torcional
Quando um corpo de prova é solicitado em torção, dois módulos de cisalhamento agem simultaneamente no caso de materiais transversalmente isotrópicos e ortotrópicos. Se a torção ocorrer como descrito na Fig. 5b, os módulos de cisalhamento atuantes são os associados aos planos cisalhados (os quatro planos laterais do corpo de prova). Portanto, o módulo de cisalhamento calculado a partir da frequência de vibração torcional fundamental corresponderá a um módulo efetivo. Assim, neste caso, o resultado obtido pelo Sonelastic® será uma combinação dos módulos de cisalhamento atuantes (a Tabela 1 indica os módulos de cisalhamento que compõem o valor efetivo para cada orientação de corpo de prova) [5].
• Coeficiente de Poisson
A caracterização do coeficiente ou razão de Poisson pela Técnica de Excitação por Impulso não é possível para materiais ortotrópicos como a madeira. Porém, a partir da Teoria da Elasticidade e utilizando a matriz rigidez, é possível obter correlações entre os coeficientes de Poisson e os módulos de elasticidade. A seguir estão descritas estas corelações (a matriz rigidez é discutida no apêndice A).
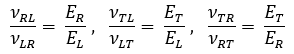
Para o cálculo dos módulos elásticos, é necessário estimar um valor para o coeficiente de Poisson. A Tabela 2 apresenta uma sugestão de estimativa e incerteza de acordo com valores médios apresentados pelas madeiras. Vale ressaltar que a sensibilidade do módulo de Young ao erro da estimativa do coeficiente de Poisson é baixa.
Tabela 2 - Coeficiente de Poisson estimado e a respectiva incerteza para o cálculo dos módulos elásticos de madeiras em função da orientação das fibras [5].
![Tabela 2 - Coeficiente de Poisson estimado e a respectiva incerteza para o cálculo dos módulos elásticos de madeiras em função da orientação das fibras [5].](/images/T2-PT-Coeficientes-Poisson-Madeiras-LT-LR-RT-RL-TR-TL-Longitudinal-Radial-Tangencial.jpg)
• Parâmetros derivados
A partir dos módulos elásticos e da densidade, é possível calcular o coeficiente de radiação sonora (R) e a impedância acústica (z) da madeira [19]. O módulo de elasticidade a ser utilizado deve ser escolhido de acordo com o modo de vibração.
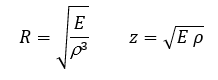
Módulos esperados para madeiras leves
As madeiras podem ser classificadas como de baixa, média ou de alta densidade. A maioria das madeiras de alta densidade apresentam valores maiores de módulos elásticos e resistência [2]. Na Tabela 3 são apresentados valores estimados para os módulos elásticos em função dos valores de EL para madeiras de baixa densidade [5].
Tabela 3 - Módulos elásticos em função de EL para madeiras de baixa densidade (valores em GPa) [5].
![Tabela 3 - Módulos elásticos em função de EL para madeiras de baixa densidade (valores em GPa) [5].](/images/T3-PT-Modulos-Elasticidade-Madeiras-Er-El-Et-Glr-Glt-Grt.jpg)
O módulo de Young determinado pela Técnica de Excitação por Impulso é dito dinâmico e sempre maior ou igual ao obtido pelo ensaio quase-estático. No entanto, é possível estabelecer uma correlação entre o módulo estático e o dinâmico. Segue abaixo um exemplo de correlação, em MPa, entre o módulo de Young determinado na direção longitudinal através de um ensaio quase-estático (ELE) e o módulo de Young determinado na direção longitudinal de forma dinâmica pela Técnica de Excitação por Impulso (ELD) [7]:

Exemplo – Madeira de eucalipto
Neste exemplo é descrita a determinação dos módulos de elasticidade de uma madeira de Eucalipto (Eucalyptus spp) em duas orientações empregando a Técnica de Excitação por Impulso e os Sistemas Sonelastic®.
Materiais e métodos
A Fig. 7 apresenta a vista superior da secção de um tronco de árvore, sendo os círculos concêntricos correspondentes aos anéis de crescimento. Nesta figura estão ilustrados três possíveis cortes para a obtenção de corpos de prova no formato de barras retangulares. Os corpos de prova indicados por (1) e (2) são os ideais para a obtenção de ET e ER, respectivamente. Em (1), a direção do comprimento consiste na direção tangencial aos anéis de crescimento e em (2), a direção do comprimento consiste na direção radial do crescimento da árvore [5].
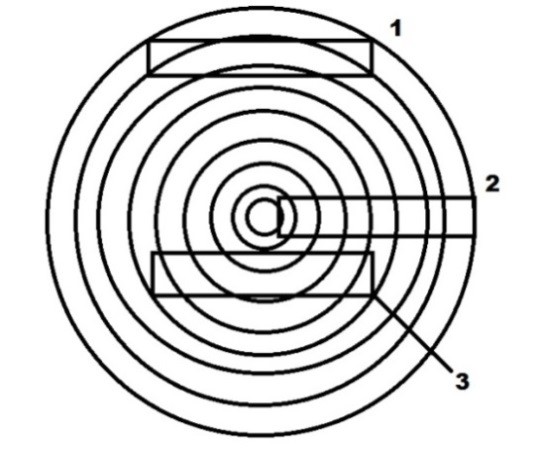
Figura 7 - Melhores locais para extrair os corpos de prova para a determinação os módulos ET (1) e ER (2). A extração em (3) combina as direções R e T.
Se o corpo de prova combina as direções R e T com indicado em (3) os valores obtidos serão efetivos e resultado de uma combinação entre ER e ET.
As Figuras 8 e 9 mostram a orientação das fibras dos corpos de prova testados. O corpo de prova da Fig. 8 possui fibras orientadas na direção do comprimento, estas barras receberam o índice “L”. Já o corpo de prova da Fig. 9 possui suas fibras orientadas na direção transversal e há uma combinação entre as direções radial e tangencial, estas barras receberam o índice “RT”.

Figura 8 - Corpo de prova com fibras na direção do comprimento (L).

Figura 9 - Corpo de prova com fibras nas direções radial e tangencial (RT).
Os corpos de prova foram ensaiados nos principais modos de vibração (flexional, torcional e longitudinal) utilizando o suporte ajustável para barras e cilindros SA-BC, o atuador eletromagnético ajustável IED, o captador acústico CA-DP e o software Sonelastic® (estes itens compõe o Sistema Sonelastic® para corpos de prova de médio porte e mostrado na Fig. 10).
Para os cálculos, foi considerado o coeficiente de Poisson estimado de 0,25 ±0,25. O coeficiente de Poisson pode variar significativamente dependendo da orientação das fibras no corpo de prova, em função disso foi considerada a incerteza ±0,25 para compreender todos os valores possíveis para esta propriedade (0,00-0,50). Nota: a influência do coeficiente de Poisson nos cálculos dos módulos elásticos é baixa, o que pode ser verificado pelas incertezas apresentadas nas Tabelas 4 e 5.

Figura 10 - Sistema Sonelastic® desenvolvido pela ATCP Engenharia Física para a determinação dos módulos elásticos de corpos de prova de madeira e derivados com a Técnica de Excitação por Impulso.
Resultados e discussões
Os corpos de prova foram organizados em dois grupos de acordo com a direção das fibras. Nas Tabelas 4 e 5 são mostrados os módulos elásticos determinados em cada modo de vibração.
Tabela 4 - Módulos elásticos dos corpos de prova “RT” determinados em função do modo de vibração.
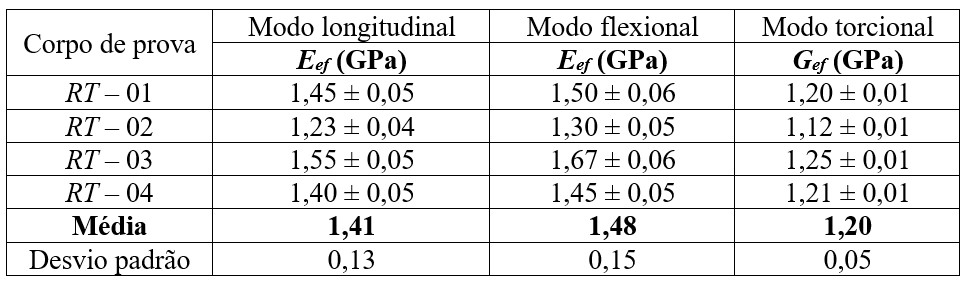
Tabela 5 - Módulos elásticos dos corpos de prova “L” determinados em função do modo de vibração.

Os módulos de Young da Tabela 4 são efetivos, pois estes corpos de prova apresentam uma combinação entre as direções R e T em seu comprimento. Já os módulos dos corpos de prova com índice “L” são denominados EL, uma vez que as fibras estão no sentido do comprimento (Tabela 5).
Nota-se uma diferença entre os módulos medidos pelo modo de vibração longitudinal e pelo flexional, principalmente para as amostras “L”. Esta diferença deve-se à presença de defeitos e descontinuidades superficiais, que influenciam mais pronunciadamente os resultados no modo de vibração flexional; também pode haver um gradiente de rigidez ao longo da espessura, de forma que a superfície seja mais ou menos rígida que o interior, influenciando os resultados. Para as madeiras há uma tendência de que as propriedades obtidas com o modo de vibração longitudinal sejam superiores às obtidas no modo flexional [10,12-14].
Por fim, o Gef consiste em um módulo de cisalhamento efetivo que combina os módulos dos diferentes planos sendo cisalhados durante a vibração. O Gef para as amostras na direção “L” é uma combinação entre GLR e GLT. Para as amostras na direção “RT” essa análise é mais complexa já que a direção principal do corpo de prova não corresponde a uma orientação bem definida (L, R ou T).
Considerações finais
A madeira e seus derivados são materiais anisotrópicos e os seus módulos de elasticidade dependem da orientação do corpo de prova e do modo de vibração empregado no ensaio pela Técnica de Excitação por Impulso. Por esta razão, a direção principal das amostras deve sempre ser levada em consideração e reportada nos resultados da propriedade avaliada.
A partir da orientação do corpo de prova e das condições de contorno para os modos de vibração flexional e longitudinal, é possível obter os principais módulos elásticos da madeira: EL, ER e ET. A Técnica de Excitação por Impulso também permite a caracterização de módulos de cisalhamento efetivos por meio do modo de vibração torcional.
Exemplos de clientes e aplicações na área de compósitos, madeiras e derivados.
Referências bibliográficas
[1] ASTM International. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration; ASTM E 1876. 2007. 15 p.
[2] DİNÇKAL, Ç. Analysis of Elastic Anisotropy of Wood Material for Engineering Applications. Journal of Innovative Research in Engineering and Science, Global Research Publishing, pp. 67-80, abr. 2011.
[3] Ponte de Madeira na floresta de Montmorency. Disponível em:
[4] Adaptado de CALIL JUNIOR, C.; LAHR, F.A.R.; DIAS, A.A. Dimensionamento de elementos estruturais de madeira. Barueri: Manole, 2003. 152 p.
[5] BODIG, J., JAYNE, B. A. Mechanics of wood and wood composites. Malabar (EUA), Krieger Publishing Company, 1993.
[6] COSSOLINO, L.C., PEREIRA, A.H.A. Módulos elásticos: visão geral e métodos de caracterização. Informativo Técnico – ATCP Engenharia Física. Out/2010. Disponível em:
[7] SEGUNDINHO, P.G.A., COSSOLINO, L.C., PEREIRA, A.H.A, JUNIOR, C.C. Aplicação do método de ensaio das frequências naturais de vibração para obtenção do módulo de elasticidade de peças estruturais de madeira. Revista Árvore, Viçosa-MG, v.36, n.6, p.1155-1161, 2012.
[8] Esquema de posicionamento e caracterização de acordo com a norma ASTM E1876. Disponível em:
[9] HEYLIGER, P., UGANDER, P., LEDBETTER, H. Anisotropic Elastic Constants: Measurement by Impact Resonance. Journal of Materials in Civil Engineering, pp. 356-363, set/out 2001.
[10] WANGAARD, F.F. The Mechanical Properties of Wood. New York: John Wiley & Sons, Inc, 1950.
[11] KAW, A.K. Mechanics of composite materials. Boca Raton: Taylor & Francis Group, 2 ed, 2006, 457 p.
[12] ROCHA, J.S., PAULA, E.V.C.M. de, SIQUEIRA, M.L. Flexão Estática em amostras pequenas livres de defeitos. Acta Amazonica, Manaus, p. 147-162. 1988.
[13] CHO, C.L., Comparison of Three Methods for Determining Young’s Modulus of Wood. Taiwan Journal for Science, pp. 297-306, Maio/2007.
[14] BUCUR, V., Acoustics of Wood. 2ª ed. Germany: Springer, 2006. p. 393.
[15] WANGAARD, F. F. The Mechanical Properties of Wood. John Wiley & Sons, Inc., New York, 1950.
[16] CALLISTER Jr., W.D. Materials Science and Engineering. 7ª ed. New York: John Wiley & Sons, Inc, 2007.
[17] Curva Tensão-Deformação. Disponível em:
< http://www.ctb.com.pt/?page_id=1471>. Acessado em: 08 de Julho de 2014.
[18] NYE, J.F. Physical Properties of Crystals: their representation by tensors and matrices. Oxford: At the Clarendon Press. 1957.
[19] Ulrike G.K. Wegst, Wood for sound. American Journal of Botany 93(10):1439-1448. October 2006.
Saiba mais sobre os Sistemas Sonelastic® :
Sistema Sonelastic® para corpos de prova de pequeno porteSistema Sonelastic® para corpos de prova de médio porte
Sistema Sonelastic® para corpos de prova de grande porte
Sistema Sonelastic® customizado e orçamento


